153P/IKEYA-ZHANG AND THE COMET OF HEVELIUS
Mark R. Kidger
Instituto de Astrofísica de Canarias
The apparition of 153P/Ikeya-Zhang = C/2002 C1
(Ikeya-Zhang) has been one of the most important cometary apparitions of recent
years. For the first time a comet with a period greater than 156 years has been
observed at more than one apparition. Despite the identification of C/1661 C1
with 153P/Ikeya-Zhang there remains the questions of the inferred major change
in the light curve between 1661 and 2002 and of the original preferred
identification with C/1532 R1, which has a strikingly similar orbit. One
possibility is that C/1532 R1 and 153P are fragments of a single object that
split in the past. A possible splitting scenario is examined. The possible
identification of previous apparitions of 153P in 837 and 1273 is examined
critically. It is shown that if these identifications are correct, the absolute
magnitude of the comet has faded considerably with time, although this in
itself may be consistent with an object that is evolving photometrically after
a major splitting.
Introduction
Comet C/2002 C1 (Ikeya-Zhang) is the first
confirmed return of a comet with a period greater than 155 years (the previous
record holder was Comet Herschel-Rigollet, last seen in 1939). Suntoro Nakano
suggested initially that the comet might be identical to C/1532 R1 but, as more
data became available, he showed that C/1661 C1 offered an even better linkage.
This linkage was later accepted as definitive, although attempts to link to
previous returns of the comet have been inconclusive, although strongly
suggestive.
Although C/1532 R1 was observed from September
2nd to December 30th. C/1661 C1 was less well observed. It was discovered on
1661 Feb. 3 in the dawn sky, just after passing perihelion, with a tail already
6º long. The comet faded rapidly and was last seen on March 28th.
The orbit used for the former in the IAU/CBAT/MPC "Catalogue of Cometary
Orbits" is that of Olbers, calculated in 1787. The orbit is not completely
determined, despite the long visibility of the comet and a 1785 solution by
Méchain gave a rather different solution, with an inclination of 42º, and an
Ascending Node of 126º. For C/1661 C1 the orbit used is the one calculated in
1785 by Pierre Méchain. These orbits are compared below to that of Comet
Ikeya-Zhang. As we can see, the similarity with the Olbers orbit of C/1532 R1
is quite impressive. The similarity with C/1661 C1 is less so; its longitude of
perihelion is very close to the corresponding value for Ikeya-Zhang, although
other parameters are not quite so close.
|
|
C/2002 C1 (Ikeya-Zhang) |
C/1532 R1 |
C/1661 C1 |
|
T |
2002 Mar. 18.9388 |
1532 Oct. 18.832 |
1661 Jan. 27.381 |
|
q |
0.507200 |
0.51922 |
0.442722 |
|
z+ |
0.017337 |
|
|
|
|
34º.5777 |
24º.53 |
33º.450 |
|
|
93º.4156 |
93º.81 |
86º.562 |
|
e |
0.991207 |
1.0 |
1.0 |
|
i |
28º.1110 |
32º.59 |
33º.015 |
On seeing this similarity, the overwhelming impression is that the three
objects may all be related and that both C/1532 R1 and C/1661 C1 may be
fragments of a single object that split in the past. The possibility of a
connection between the comets of 1532 and 1661 seems first to have been
appreciated by Halley, in his “A Synopsis of the Astronomy of Comets” of 1705,
who suggested that they were in fact one and the same comet. But what then of
the initially favoured identification of 153P/Ikeya-Zhang with C/1532 R1? Could
the comet of 1532 and the 1661-2002 comet be fragments that split from each
other in the distant past? The similarity of the orbital elements seems to
suggest so. Based on Nakano’s Feb 25 1661-2002 linked solution, the previous
calculations indicated that the apparition prior to 1661 occurred in 1273
April/May. Given that a comet is recorded in the Chinese annals as being first
sighted on 1273 April 9, it is reasonable to ask whether this is in fact
another record of Ikeya-Zhang or merely a coincidence. What leads us to the
former opinion is that the details given of the comet’s apparent motion mimic
rather well the expected track of Ikeya-Zhang if its perihelion passage were
about a month earlier than that indicated by the preliminary calculations.
The comet of 1273 was first seen by the Chinese at the ecliptic longitudes
of the Hyades and to the ‘north’ of Auriga. This latter is rather imprecise but
still useful for our purposes. Of more use is the statement that the comet
subsequently passed from the asterism 28/n/f/q/15 UMa and then penetrated
the ‘ladle’ of the Plough. This piece of information effectively limits an
Ikeya-Zhang type orbit to having a perihelion passage time between March 26.5
and 28.5. The record then goes on to say that the comet passed through Bootes
and reached the region of p Boo. All of this
happened, according to Ho’s translation, in 21 days. For our orbit this track
would be covered in two months and the end point would be nearer to h Boo. To a certain extent,
such details are negotiable (due to possible copying errors etc.) but the time
period is something of a problem, as is the visibility for the extended period
if the comet were indeed Ikeya-Zhang with its current absolute magnitude.
In spite of the possible identification problems we now assume that the
comet of 1273 was indeed Ikeya-Zhang and see how it can help us in our quest to
reconcile C/1532 R1 with Ikeya-Zhang. We take as starting point the MPEC 2002-F55
orbit solution and then introduce non-gravitational terms into the integration
to move the previous perihelion time from mid-1662 to 1661 Jan 28.900. This can
be achieved by any number of possible pairings of the non-gravitational
parameters A1 and A2, as shown in the table below which gives sample sequences
of perihelion passage times derived by integration from the 2002 epoch.
|
A1 = |
0.626925 |
0.60723 |
0 |
|
A2 = |
0 |
-0.0062435 |
-0.198742 |
|
|
|
|
|
|
1661 Jan. 28.90 |
1661 Jan. 28.90 |
1661 Jan. 28.90 |
|
|
1273 Apr. 26.2 |
1273 Mar. 27.7 |
1270 Sept. 24.8 |
|
|
879 Jan. 5 |
877 Aug. 7 |
798 May 3 |
|
|
426 Nov. 3 |
451 Oct. 22 |
314 Mar. 2 |
|
|
-61 July 16 |
-59 Nov. 8 |
-155 Feb. 25 |
By including
nongravitational effects in his 1661-2002 linked solution Nakano (April 15)
initially found A1 = 1.76 and A2 = -0.0129, leading to perihelion passages of
1661 Jan 29, 1273 Feb 23, 877 July 7 and 452 Oct 23. A recent revision of this
by Nakano (April 26) gives A1 = 1.64 and A2 = -0.0163 - resulting in a sequence
of previous perihelia of 1661 Jan 29, 1273 Feb 7, 877 Feb 23, and 458 July 31.
Although there are many possible combinations of A1 and A2 that will give
the desired result as regards 1661, if we want to force a fit to our possible
1273 comet at the same time then the options become rather limited. For
instance, if we were to want to fit to, say, T = 1273 Mar. 30 then the orbit
prior to 454 would have been hyperbolic due to a close (0.12au) approach to
Jupiter. However, a close approach to Jupiter in the 5th Century
would be an attractive scenario for causing a splitting of the nucleus. Given
that the window of solution for the 1273-1661-2002 linkage is very limited
around 450 due to the position of Jupiter, it seems reasonable to assume that
the splitting occurred around this time in order to take advantage of the
Jovian perturbations about 400 days after perihelion passage. Also, if we
assume that the splitting actually occurred at perihelion then the difference
in the assumed non-gravitational effects will have separated the two fragments
by enough to produce useful differential Jovian perturbations when the
fragments pass through their descending nodes.
As we will see though, other scenarios are perfectly possible too.
Less attention
has been paid to linkage by Nakano to 877 despite the fact that this was his
initial linkage to the 1661-2002 observations, which then permitted linkage
between 877, 1661 and 2002.
The Japanese record a Guest Star in Pegasus that appeared on February 11th (Ho 307). A comet was also observed in the west from Europe for 15 days in March and a comet in China in June & July (Pingré 349). However, a “Guest Star” (ko-hsing) was usually a nova, especially if no movement was recorded. In oriental chronicles a comet was a “hui-hsing” if tailed and a “po-hsing” if not, thus there must be considerable doubt about the suggestion that the object was a comet.
Nakano links the Japanese and European observations with 153P, although he uses only a single position for the Guest Star in Pegasus. Support for the comet interpretation though can be garnered from the fact that Pegasus is at sufficiently high galactic latitude to make a nova unlikely, if certainly not impossible. Yeomans states that the European comet was seen in Libra, in the south-west in the morning sky. Nakano’s linkage puts the comet in eastern Cygnus, in the eastern sky at dawn! Theoretically it was just visible at magnitude 3 at this time in the north-west at sunset from northern Europe, but very low in a very bright sky. It looks very unlikely that it would have been observed in the evening sky, but would have been easy at dawn.
Thus, while the
linkage with the comet seen in 1273 looks highly plausible, there are real
difficulties with the linkage to 877 and it is far from certain that the
objects recorded by Ho and by Pingré are one and the same.
Clues in the light curve
C/1532 R1 was evidently an exceptional object.
David Hughes's 1987 catalogue of cometary absolute magnitudes from 568 - 1978
assigns it an absolute magnitude of +1.8, one of just 12 comets that has an
absolute magnitude of +2 or brighter, putting it into the "giant
comet" class, almost 100 times intrinsically brighter than the average
long-period comet. In contrast, C/1661 C1 is a more normal object. David Hughes
lists its absolute magnitude as +4.6, much closer to that of Ikeya-Zhang,
particularly as the observations suggest that the comet became diffuse and
faded out rapidly.
The light curve fit to C/2002 C1 (Ikeya-Zhang)
from the observations in the archive of The Astronomer magazine
(provided by courtesy of Guy Hurst) – below – suggests an absolute magnitude of
7.2, slightly fainter than average for a "new" comet.
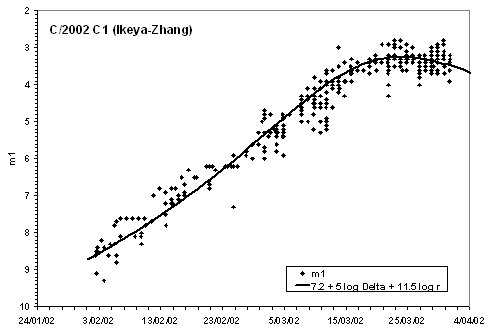
This leads to an immediate problem: 153P/Ikeya-Zhang was very much fainter intrinsically than either C/1532 R1 or C/1661 C1. The 1661 light curve mystery is an important part of the problem of linkage. A look at the observational circumstances for 153P/Ikeya-Zhang in 1660/61 shows that, of the four returns that are treated here this was the most favourable. The comet was bright and had excellent pre-perihelion visibility, yet neither Hevelius, nor any other observer recorded it in the evening sky.
|
Date |
Comet |
m1 |
Sun |
Moon |
|
31/12/1660 |
14º |
+3.0 |
-17º |
New |
|
05/01/1661 |
15º |
+2.6 |
-16º |
Crescent |
|
20/01/1661 |
12º |
+0.7 |
-14º |
Waning |
|
23/01/1661 |
9º |
+0.4 |
-13º |
Last Quarter |
Hevelius would have had two chances to discover
the comet pre-perihelion in the evening sky if it was as bright as we believe:
- In
late December-early January around New Moon at magnitude 2.5-3 in a dark
sky.
- After
the January 15th Full Moon around magnitude +0.5 in twilight.
Even if the comet had been missed in late
December when it would have been low in the west after sunset in a practically
dark sky, with a magnitude around +3, the comet would have been very bright and
extremely obvious low in the twilight, after the end of nautical twilight (i.e.
with only the horizon lit) after the January full moon. Even assuming
widespread bad weather, if the comet was as bright as thought it would have
been seen by someone before perihelion and would have been bright enough to be
widely observed by the general public.
John Bortle (Bortle, J.: 2002, TA, 38, 455,
298) argues convincingly that the best solution for the apparent discrepancy
between the brightness of the 1661 and the 2002 returns of Comet Ikeya-Zhang
may be a strong perihelion asymmetry in the light curve of the comet. Such an
asymmetry would have important dynamical implications for the comet's orbit too
and would significantly affect extrapolations of the orbit into the past. Even
if we invoke the enduring photometric effects of a splitting event at a
previous perihelion passage that would gradually diminish with time and could
account for the comet having a significantly brighter absolute magnitude at a
previous return.
However, the observed light curve shows that
the degree of perihelion asymmetry at the 2002 return was very small.. The main
conclusions of the study of the extensive The Astronomer data archive
are that:
1.
There
is only a very slight perihelion asymmetry amounting to no more than 0.2
magnitudes.
2.
Peak
brightness was attained approximately 2 days after perihelion.
3.
The
peak brightness of the innermost coma as measured by CCD photometry in a 10
arcsecond aperture was reached approximately a week before perihelion.
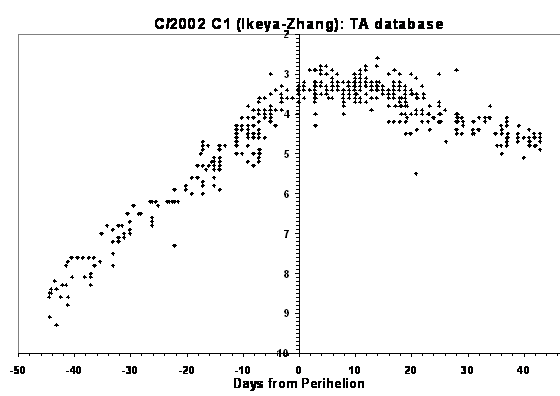
The complete TA archive up to the end of March
with the fit to the light curve derived from the sample of data used in the
April TA is shown left. Although not perfect, the fit obviously gives a good
approximation to the light curve.
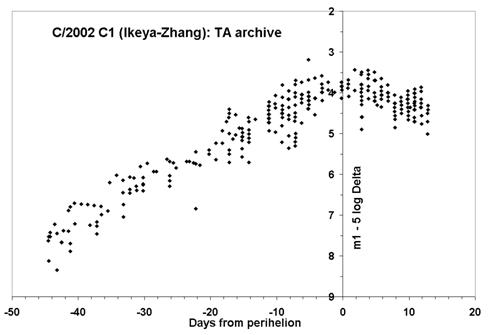
The peak brightness of the comet was approximately magnitude 3.5 in the days just after perihelion. However, as the geocentric distance was decreasing at that time, the date of peak apparent brightness and that of the true peak brightness are not the same. To correct for this we subtract 5*log D from the apparent magnitudes to shift them to a standard geocentric distance of 1AU. This plot is shown here. The dispersion in the plot is around 0.8 magnitudes, but it does appear that the true peak brightness is shifted very slightly to the right of the axis (i.e. post-perihelion). The effect is 2±1days.
This shows that there was no large perihelion
asymmetry in the light curve. It also implies that the simplest form of the
non-gravitational terms, as expressed in Graeme's accompanying article, may be
a good approximation to the true situation in C/2002 C1 (Ikeya-Zhang), although
he notes that even a very small perihelion asymmetry can have important
dynamical implications (an order of magnitude estimate is that a 1 day
asymmetry in the non-gravitational term leads to a 3 month change in the
perihelion date at the last return.
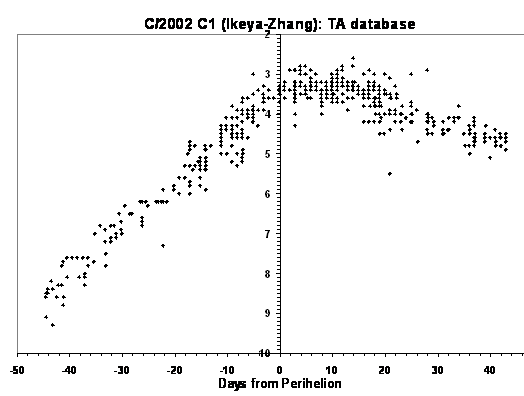
Note that the TA database confirms that the
comet has been significantly brighter post-perihelion than pre-perihelion. The
fit to the light curve (above) shows that the best fit to the data has a
brightening rate that is very similar, but with the post-perihelion data
systematically 0.4 magnitudes brighter. Some caution must be applied to the
rate of fade post-perihelion as the brightening event observed in the light
curve in late April significantly flattens the apparent rate of fade. When
these data are ignored the rate of brightening pre-perihelion is
indistinguishable from the rate of fade post-perihelion. The comet is found to
have shown a 0.5 magnitude brightening in late April that continued for some 3
weeks. At the peak of this event the comet was actually brightening in real
terms as the heliocentric distance increased.
Investigation of the data shows that the small
perihelion asymmetry in the date of maximum brightness may be due to the phase
angle term. In other words, shadowing of dust grains in the coma. The plot
below was prepared as a test from on-line ICQ data that was made to assess the
possible size of the effects of perihelion asymmetry on the non-gravitational
terms. The residuals from the best light curve fit are shown. Note that in the
top plot there is a significant trend to brighter magnitudes post-perihelion.
When a phase angle term is included the residuals flatten out although two
interesting effects are seen. Note that the comet brightens quite significantly
from mid-April. There is also a possible
sinusoid in the residuals that has been noted in other data sets. This shows
the characteristic signature expected from a precession of the nucleus with a
period of approximately 6 weeks. However, to confirm this feature will require
a very much longer data set probably at least double the one shown here.
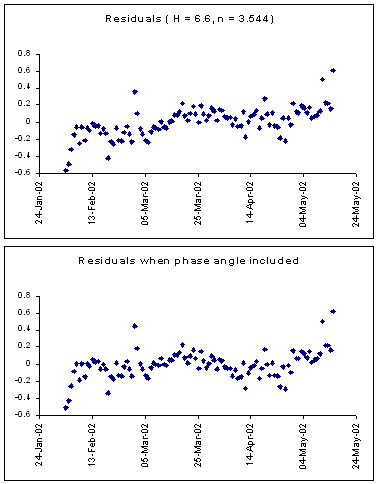
It is of interest to note that recent data
shows that the morphological behaviour of the comet has reproduced an effect
seen in Hevelius's comet of 1661. As commented in the March TA, Hevelius's
comet became very large and diffuse and faded out rapidly. This effect was
present in C/2002 C1 (Ikeya-Zhang). Visual observations in May 2002 showed that
the coma was half a degree or more across and extremely diffuse, with DC=0-1
such that became difficult to observe despite remaining a relatively bright
object. The coma diameter estimates give a consistent linear diameter of 250
000km around perigee in late April, but that by June 10th the coma
measured 1.3-1.5 million kilometres in diameter.
The brightening event in late April 2002 is
interesting. It could be interpreted as a perihelion asymmetry, although it is
too little too late to explain Hevelius’s observations in 1661 (and his lack of
observations pre-perihelion). If we fix “n” and allow “H0” to vary
we obtain the following curve:
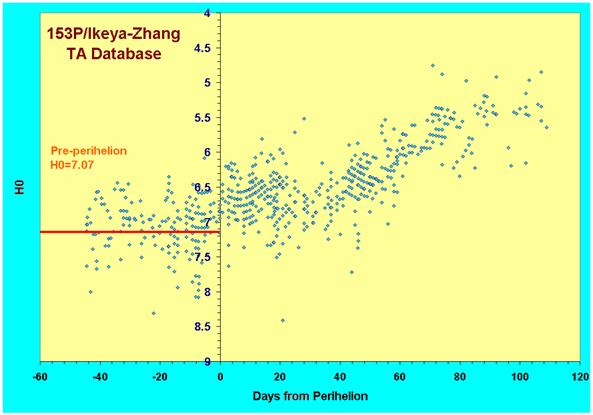
We see that H0 brightens from 7.07
at perihelion, to approximately 5.4, but this brightening starts at around
T+35d, far too late to explain the presumed light curve in 1660/61. This
brightening is also of too small amplitude to explain the lack of visibility in
late January 1661, even if it were to have initiated much earlier relative to
perihelion.
The light curve suggests that there are
problems with the identification of a comet seen by the Japanese and Koreans as
being the same as the Chinese comet.
Ho’s comet
catalogue lists a broom star seen by the Japanese (Feb. 5) in the evening sky
and the Koreans (Feb. 17) in the morning sky.
As we have
seen, the Chinese saw a “bluish white guest star with the appearance of loose
cotton” (a classical description of a tailless comet) in Auriga on Apr. 9th.
– Ho lists
the two as identical (Ho 439), although their position and movement seems
incompatible with this.
– Nakano
links the former with 153P/Ikeya-Zhang (T = 1273 Feb. 4.8) based on the
evening-morning shift.
This suggests that there may be a transcription
error in the date(s) of observation of the Japanese/Korean comet, as there was
in the 4BC “Star of Bethlehem” event.
If we assume that the comets of 877, 1273 and
1661 had the same light curve as the observed light curve of 153P/Ikeya-Zhang
in 2002, we find that the problem of visibility and compatibility with the
observed dates of observation becomes progressively worse.
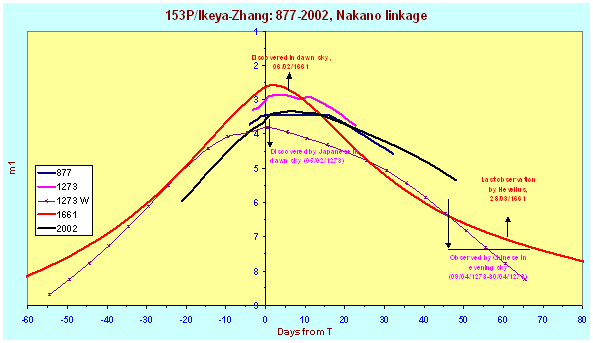
We see that, for example, in the Waddington
linkage to the 1273 apparition, we see that the comet would, given the 2002
light curve, barely pass magnitude +4 and in 877 would only reach 3.5, whereas
it is evident that at both returns the comet was much brighter than that. Both
Nakano and Waddington’s linkage suggest that the comet would have been barely
naked eye visible when observed by the Chinese in the evening sky. However, the
Chinese observation of colour in the comet suggests that it was very bright. If
the Waddington linkage is correct the comet would have been magnitude 1.5 and
fading at discovery, even if it was as bright as Hevelius’s comet in 1661 and
thus too faint to show colour!! We must assume then that it was even brighter
in 1273 than in 1661.
This suggests that there has been a systematic
fade of the comet since at least 1273, which is consistent with post-splitting
activity.
What if C/1532 R1 and 153P/Ikeya-Zhang are fragments of a single comet that split in the 1st Century AD? The very bright (m0= 1.8) comet of 1532 would be the principal nucleus. The descending node of 153P is close to Jupiter’s orbit and permits very close encounters. A post-split encounter with Jupiter could separate the nuclei allowing returns of the fragments in 1532 and 1661. There are many possible scenarios, but one would have a splitting during an apparition in 58AD, followed by an encounter with Jupiter in 458AD that separated the fragments in T.
Conclusions:
Although the 1661-2002 linkage is firm, there
are major problems with the linkages to 1273 and to 877, although the evidence
of a linkage to the Chinese comet of 1277 is strongly suggestive. The evidence
suggests that the comet has faded significantly over its last 3 apparitions.
This is consistent with 153P/Ikeya-Zhang being the smaller fragment of a comet
that split early in the first millennium AD. Comet C/1532 R1 would be the
principal nucleus of the split comet. If this scenario is correct we can expect
this nucleus to return in the late 21st Century.
Author’s Note: This text is based on a series of articles
published in The Astronomer magazine by Mark Kidger and Graham Waddington
between March and June 2002. The author is grateful to Graham Waddington for
many long and fruitful discussions and for his collaboration in the articles in
The Astronomer.